Лабораторна робота № 5

Тема: Суматори

Мета: Ознайомитись з логічними елементами та навчитись проектувани найпростіші логічні схеми.

Обладнання: Комп'ютер.

Теоретичні відомості:

Суматор є найпростішим цифровим пристроєм. Це вузол ЕОМ, що виконує арифметичне підсумовування кодів чисел, тобто він призначений для додавання двох чисел, заданих у двійковому коді. Зрівняємо підсумовування десяткових і двійкових чисел:

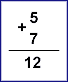
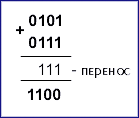
Правила додавання двійкових і десяткових чисел однакові:

додавання виконується порозрядно – від молодшого розряду до старшого;

у молодшому розряді обчислюється сума молодших розрядів що складають Aі та Bj. Ця сума в даній системі числення може бути записана однозначним числом S1 або двозначним числом P1S1. Функція P називається переносом;

у всіх наступних розрядах знаходиться сума даних розрядів доданків Аі та Bі, причому при Pi-1=1 до цієї суми додається одиниця (у числових прикладах, наведених вище, цей випадок виділений жирним шрифтом, результат додавання в і-му розряді записується у вигляді однозначного Sі, або двозначного PiSі числа.

Таким чином, у кожному розряді необхідно знайти суму Аі, Bі і Рі-1 (якщо Рі-1=1), тобто визначити Sі й Pj. По числу входів розрізняють напівсуматори, однорозрядні суматори (ОС) і багаторозрядні суматори.

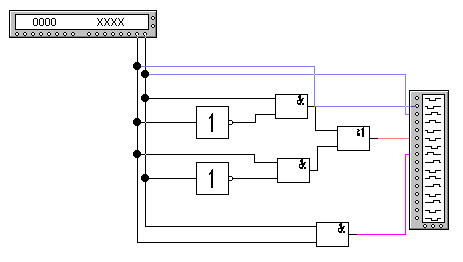
Рис.1. Схема напівсуматора

Напівсуматорами називаються пристрої з двома входами й двома виходами, на яких виробляються сигнали суми й переносу. Напівсуматор реалізує лише частину завдання підсумовування, тому що не враховує вхідної величини – переносу із сусіднього молодшого розряду в даних (див. рис. 1 та рис. 2).

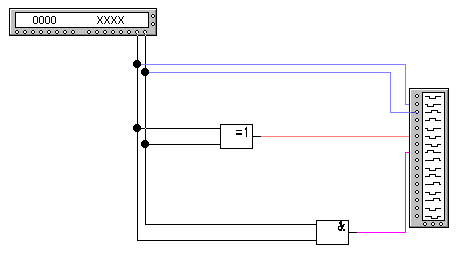
Рис. 2. Схема напівсуматора з використанням стандартної схеми додавання по модулю 2

У таблиці 1 наведена таблиця істинності напівсуматора. На рис. 3 наведена часова діаграма роботи напівсуматора.

Таблиця 1. Таблиця істинності напівсуматора

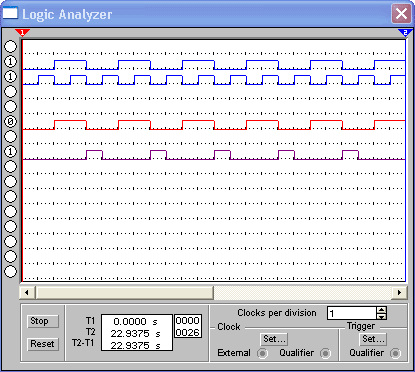
Рис. 3. Діаграма роботи напівсуматора

Логічні рівняння: S=x^*y+x*y^ P=x*y

Однорозрядний двійковий суматор складається із двох комбінаційних схем: одна формування Si, друга для визначення Pі. (див. рис. 4 та рис. 5). Багаторазрядний суматор будується на основі однорозрядних відповідно до правил додавання.

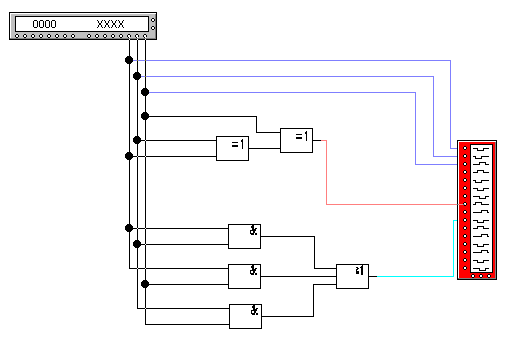
Рис. 4. Схема однорозрядного двійкового суматора

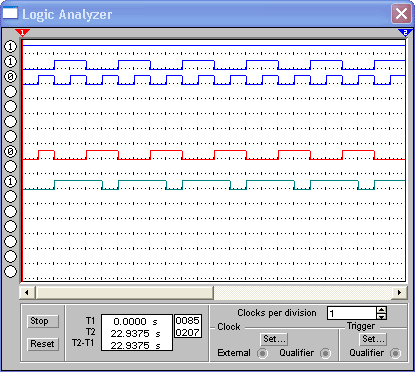
Рис. 5. Діаграма роботи однорозрядного двійкового суматора

Однорозрядні суматори мають три входи й забезпечують додавання розрядів доданків і перенос із попереднього розряду (див. табл. 2).

Таблиця 2

Таблиця істинності суматора

Логічні рівняння:

Мінімізуючи дані рівняння за формулами алгебри логіки, побудуємо суматор в Electronics Workbench.

Залежно від характеру вводу-виводу кодів та організації переносів, багаторозрядні суматори бувають послідовного й паралельного принципу дії.

У послідовному суматорі додавання кодів здійснюється порозрядно, починаючи з молодшого розряду за допомогою комбінаційного суматора на три входи. Перенос, що утвориться в даному розряді, Pj+1 затримується на час tод і надходить на вхід Pj суматора в момент надходження наступного розряду доданків. Таким чином, послідовно розряд за розрядом виконується додавання кодів чисел. Перевагою послідовного суматора є простота апаратурної реалізації, а недоліком – досить великий час підсумовування (див. рисунок 6).

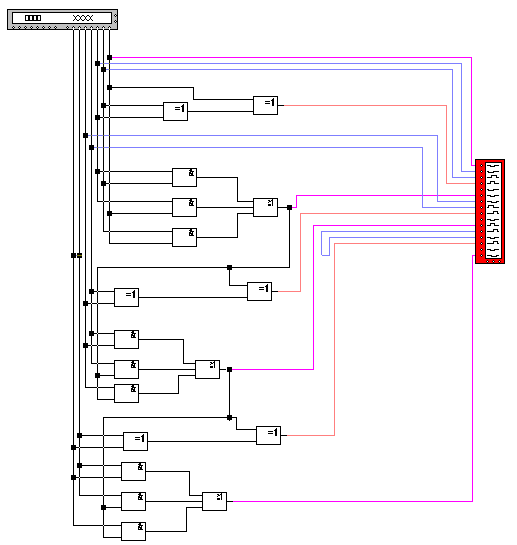
Рис. 6. Схема послідовного суматора

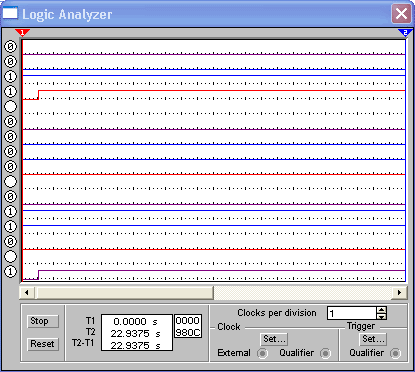
На рис. 7 наведена часова діаграма, що ілюструє роботу послідовного суматора.

У паралельному суматорі досягається більш висока швидкодія. Коди, що додаються, надходять на вхід суматора одночасно по всіх розрядах. Для цього в кожному розряді використовується комбінаційний суматор на три входи, на виходах якого утворяться значення суми Sj даного розряду й переносу Pj+1 у старший розряд. У процесі поширення сигналу переносу встановлюється остаточне значення суми в кожному розряді. Очевидно, що протягом цього часу на входах суматора присутні сигнали Xi, Yi, що відповідають сумуючим кодам. Максимальне за час підсумовування виходить у тому випадку, коли перенос, що виник у першому розряді, поширюється по всіх розрядах (наприклад, при додаванні кодів 11..11 та 00..01). У паралельному суматорі звичайно застосовуються різні способи прискорення переносу (паралельний перенос, груповий і т.п.).

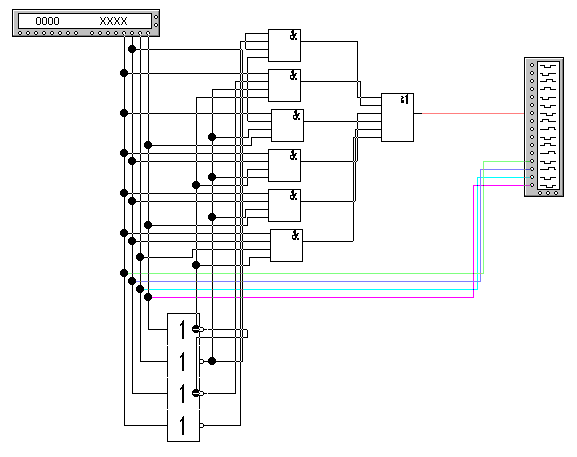
Рис.8. Схема паралельного суматора

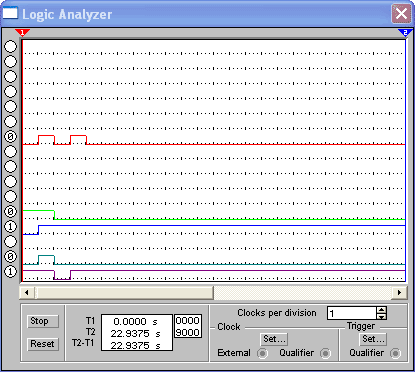
На рис. 9, наведена часова діаграма, яка ілюструє роботу паралнльного суматора .

Цифрові схеми порівняння формують на виході F=1 при рівності двох двійкових чисел А, що подаються на вхід, (порозрядно записуємо а й b) і В (с і d). Цифрова схема порівняння – це цифровий аналог компаратора (див. рис. 8), що є одним з найважливіших пристроїв імпульсної техніки, часова діаграма суматорів наведена на рис. 9 На основі таблиці істинності для компаратора складемо рівняння (для A>B, A<B, A=B), мінімізуємо їх, використовуючи закони алгебри логіки (див. табл. 3).

Таблиця 3. Таблиця істинності цифрової схеми порівняння

Логічні рівняння:

A>B = a^bc^d^ + ab^c^d^ + ab^c^d + abc^d^ + abc^d + abcd^
A<B = a^b^c^d + a^b^cd^ + a^b^cd + a^bcd^ + a^bcd + ab^cd
A=B = a^b^c^d^ + ab^cd^ + a^bc^d + abcd

Завдання:

Використовуючи пакет Electronics Workbench, спроектувати схему на основі найпростіших елементів, використовуючи для складання схеми таблицю істинності й проаналізувати роботу суматора або схеми порівняння.

Скласти звіт про виконання лабораторної роботи , в який включити:

схеми, побудовані в Electronics Workbench;

часові діаграми роботи виконаних вами схем.

Загальне завдання:

1.спроектувати однорозрядний суматор.

2.спроектувати чотирьохрозрядний суматор з послідовним переносом;

3.спроектувати цифрову схему порівняння дворозрядних двійкових чисел A<B;

4.спроектувати цифрову схему порівняння дворозрядних двійкових чисел A>B;

5.спроектувати цифрову схему порівняння дворозрядних двійкових чисел A=B.

Electronics Workbench
копія інформації  з сайту